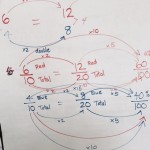
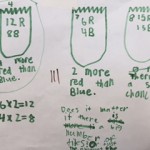This project investigated how teaching practices can be enhanced through focusing on eliciting and building upon students’ mathematical thinking. Being inspired by the notion that “we understand something if we see how it is related or connected to other things we know” (Hiebert and Carpenter, 1992, p. 4), we set out to co-plan, co-teach and research how other educators focus on students’ mathematical thinking. In particular, we grounded our project in the research about formative assessment and inquiry-based teaching. The co-teaching occurred in three junior classes on probability, geometry and measurement.
Team Members
Marc Husband
Toronto District School Board
John Goodyear
Toronto District School Board
Sheila Delaney
Toronto District School Board
Ann Weir
Toronto District School Board
Tina Rapke
York University
Professional Learning Goals
We enhanced our teaching practices in the following ways:
- we adopted and modified Stein and Smith’s five practices for orchestrating mathematics discussions in the classroom
- followed recommendations from formative assessment literature (e.g., Black and Wiliam, 1999) to adjust our in-class teaching actions based on what students shared
- aligning our practices with inquiry-based learning philosophies (i.e., student-centred methods)
Activities and Resources
We met with graduate students that were enrolled in a mathematics education course from York University. They helped us identify and gain familiarity with the research that related to our professional learning goals. The graduate students also helped us co-plan our lessons by basing the tasks on literature pertaining to geometry, probability and measurement. We opened our classrooms to both teachers and graduate students, video recorded our lessons, and collected student work samples. The graduate students and ourselves analyzed and identified student samples that evidenced mathematical understanding. Student work samples and video data were analyzed based on the definition that “we understand something if we see how it is related or connected to other things we know” (Hiebert and Carpenter, 1992, p. 4).
Unexpected Challenges
Upon reflection of our entire project experience, we would like to further develop and adapt some of the roles enacted while co-teaching (e.g., the annotator, the whisperer and the questioner). We need more time in each other’s classrooms to refine our process of co-teaching.
We did find it difficult to talk about our classroom practices that were used to elicit and build upon student thinking. The literature is lacking specific nuances of how these practices play out moment-by-moment. We have found some promising research that we would like to explore. We feel that the Towers and Proulx’s (2013) notion of “coordinating the possible” (p. 21) could be useful. Having and developing language would allow us and other teachers to describe and ultimately lead to further enhancements of classroom practices.
Enhancing Student Learning and Development
We found evidence of student mathematical understanding in the data we collected – please see student work samples.
Sharing
We have crafted a proposal that we will submit in hopes to present at next year’s OAME conference (2016). We are currently crafting a manuscript (collaborating with graduate students and their instructor) to submit for publication in a peer-reviewed research journal. Our results and experiences have been shared with our colleagues at staff meetings. Sheila Delaney will be the math lead for our school next year, and she is planning on drawing upon our project experiences in her new role.
Project Evaluation
The release time allowed us to spend time doing the math, becoming familiar with related research, discussing a variety of tools and strategies, annotate each other’s thinking, revisit the problem, and provide each other with feedback on our teaching. This positioned us very well to replicate these math understandings and instructional practices in our classrooms and to reflect on our teaching while we met. We measured the success of our new practices by identifying students’ mathematical understanding in their work samples.
Resources Used
Stein, Mary Kay, and Margaret S. Smith. (2011). 5 Practices for Orchestrating Productive Mathematics Discussions. National Council of Teachers of Mathematics. 1906 Association Drive, Reston, VA 20191-1502.
Black, Paul, and Dylan Wiliam. (1998). Assessment and classroom learning. Assessment in education, 5(1), 7-74.
Black, Paul, Dylan Wiliam and Assessment Reform, G. (1999). Assessment for learning: beyond the black box. Cambridge: University of Cambridge Institute of Education.
Wiliam, Dylan and Judith Reed. “What Does Research Say the Benefits of Formative Assessment Are?” Research Brief. VA: NCTM, 2007.
Ontario Ministry of Education Capacity Building Series: Inquiry-based Learning.
https://www.edu.gov.on.ca/eng/literacynumeracy/inspire/research/CBS_InquiryBased.pdf
Ebby, C., Ottinger, M., & Silver, P. (2007, October). Improving mathematics instruction through classroom-based inquiry. Teaching Children Mathematics, 14(3), 182-186.
National Council of Teachers of Mathematics (NCTM). Principles and Standards for School Mathematics. Reston, VA: NCTM, 2000.
http://www.nctm.org/Standards-and-Positions/Principles-and-Standards/
Nicolson, C. P. (2005). Is chance fair. Teaching Children Mathematics, 12(2), 83.
Towers, J., and Proulx, J. (2013). An enactivist perspective on teaching mathematics – Reconceptualizing and expanding teaching actions. Mathematics Teacher Education and Development, 15, 5-28.
Resources Created
These resources will open in your browser in a new tab, or be downloaded to your computer.